Stefan's Law of Radiation

Calculate the energy radiated in one minute by a blackbody of surface area $200 {\mathrm{cm}}^2$ at $127 ° \mathrm{C}$ $\left(\sigma =5.7\times {10}^{-8} \mathrm{J} {\mathrm{m}}^{-2}{\mathrm{s}}^{-1}{\mathrm{K}}^{-4}\right)$.

Two spherical objects $A\&B$ are at temperature $T_A$, $T_B$. If $E_A$ and $E_B$ are the power radiated by body $A$and$B$, then value of $\frac{E_A}{E_B}$ will be (given temperatures $T_A=2T_B$, Radius$2R_A = R_B$, $e_A= 0.5e_B$, $e_A$and $e_B$ are the emissivity of $A$ and$B$)

The ratio of emissivities of two bodies is $\frac{e_1}{e_2}=\frac{1}{81}$. Bodies have same surface area and emit total radiant power at the same rate. Find the ratio of wavelengths corresponding to maximum spectral radiance $\frac{{\lambda }_1}{{\lambda }_2}$

There are two parallel infinite black sheets maintained at temperatures $T_{1 }\left(K\right)$ and $T_2$ ($K$). The temperature of a third, identical sheet placed midway and parallel to the sheets at equilibrium will be:

A perfectly black body having area $1{\mathrm{cm}}^2$ is heated to a temperature $1000 \mathrm{K}$. The amount of energy radiated by it in $1 \mathrm{s}$ is (in $\mathrm{J}$)

(Stefan' constant=$5.67\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2} {\mathrm{K}}^{-2}$)

A tungsten lamp at a temperature of $3000 \mathrm{K}$ has surface area of $0.3 {\mathrm{cm}}^2$. If the lamp has emissivity of$0.4$, the rate of heat radiated is
 

The ratio of masses of two metal spheres A and B is $8:1$. If their temperature are $2000 \mathrm{K}$ and $1000 \mathrm{K}$respectively then the ratio of the rates of their energy emission will be

Two spheres of radii $r_1$ and $r_2$ have densities ${\rho }_1$ and ${\rho }_2$ and specific heats $C_1$ and $C_2$ respectively. If they are heated to the same temperature, the ratio of their rates of fall of temperature in the same surroundings will be

A sphere, a cube and a thin circular plate, all made of the same material and having the same mass are initially heated to a temperature of $900°\mathrm{C}$. Which one of the following will cool first?

A point source is at temperature $T$. The intensity at a point at a distance $r$ is $I$. The temperature is doubled and the distance of point is also doubled. The intensity will become

A sphere of surface area $4 {\mathrm{m}}^2$ at temperature $400 \mathrm{K}$ and having emissivity $0.5$ is located in an environment of temperature $200 \mathrm{K}$. The net rate of energy exchange of the sphere is

(Stefan Boltzmann constant $\sigma =5.67\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2} {\mathrm{K}}^4$)

If the absolute temperature of a black body is doubled the percentage increase in the rate of loss of heat by radiation is

A heater is placed inside a hollow sphere of surface area $4 {\mathrm{m}}^2$ and emissivity $0.2$. This sphere is enclosed by another hollow sphere of surface area $15 {\mathrm{m}}^2$ and emissivity $0.8$. The bigger sphere is surrounded by vaccuum. If temperature of smaller sphere in steady state is $600 \mathrm{K}$ then  (Take : $\sigma =\frac{17}{3}\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2} {\mathrm{K}}^{-4}$):

A point source of light of power $P_0$ is placed at a distance of $4 \mathrm{m}$ from the centre of a thin hemispherical shell as shown in the figure, The shell has a radius of $3 \mathrm{m}$ and it behaves like a perfect black body. If the temperature of the hemisphere is related to the power of the source as $T^4=\frac{P_0}{n\pi \sigma }$' where $\sigma$ is the Stefan's constant, then find the value of $\frac{n}{10}$.

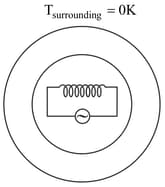
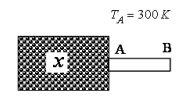
A solid body $x$ of very large heat capacity is kept in an atmosphere whose temperature is $T_A=300 \mathrm{K}$ The body $X$ is connected to a rod of length $1 \mathrm{m}$ and cross sectional area $S$, as shown in the figure. Thermal conductivity of rod $AB$ is $0.0567 \mathrm{W} {\mathrm{mk}}^{-1}$. Assuming that there is no heat exchange with the surrounding except end $B$ of the rod i.e., neither by any surface of $X$ nor by the curved surface of rod. The end $B$ has emissivity $e=0.8$. The rod $AB$ is radiating heat through the end $B$ only. If the steady state temperature of the end $B$ is $400 \mathrm{K}$ then find the temperature(in $\mathrm{C}°$) of $X$ at the steady state. (Stefan Boltzmann's constant $\sigma =5.67\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2}{\mathrm{k}}^4$)

Two identical large 'thin' metallic sheets each behaves like a black body are kept parallel to each other with small separation between them in vacuum. Thermal energy is generated at a constant rate $3 \mathrm{kW}$ in one of the sheets by a passing electricity in it. In steady state, temperature of the other sheet is found to be a constant. Find this temperature. (Given area of the plates $A=\frac{{10}^3}{17\times 27}{ \mathrm{m}}^2$ and Stefan's constant $\sigma =\frac{17}{3}\times {10}^8 W {\mathrm{m}}^{-2}{ K}^4)$

Two identical metallic sheets each behaves like a black body are kept parallel to each other with small separation between them in vacuum. Thermal energy is generated at a constant rate $P$ in one of the sheets by a passing electricity in it. In steady state, temperature of the other sheet is found to be constant is $300 \mathrm{K}$. Find the value of $P$ in Kilo-Watt.
(Given area of the plates $A=\frac{{10}^3}{17\times 27}{ \mathrm{m}}^2$ and $\sigma =\frac{17}{3}\times {10}^{-8}\mathrm{w} {\mathrm{m}}^{-2}{ \mathrm{K}}^4$)

A spherical black body has a radius $R$ and steady surface temperature $T$, heat sources ensure the heat evolution at a constant rate and distributed uniformly over its volume. What would be the new steady surface temperature of the object if the radius is decreased by half? Assume surrounding to be at absolute zero and heat evolution rate through unit volume remain same.

The distance of the earth from the sun is $4$ times that of the planet mercury from the sun. The temperature of the earth in radiative equilibrium with the sun is $290 \mathrm{K}$. If the radiative equilibrium temperature of the mercury is $T$, (Assume all three bodies to be black body) find $\left(\frac{T}{290}\right)$.

An iron wire of diameter $1 \mathrm{mm}$ and length $10 \mathrm{cm}$ is placed in an evacuated chamber. Assume that all heat transfer is by radiation and that the surface of wire radiates according to Stefan's law. Take the temperature of the chamber to be ${27}^{°}\mathrm{C}$. Specific resistance of the wire is $10\times {10}^{-8}\Omega -\mathrm{m}$. (Take the emissivity of iron wire is $1$). Choose the correct statement(s).